Plasmonics
Plasmonic Nanoparticles
Plasmonic metal nanoparticles – including gold, silver, and platinum – are highly efficient at absorbing and scattering light. By changing nanoparticle size, shape, and composition, the optical response can be tuned from the ultraviolet through the visible to the near-infrared regions of the electromagnetic spectrum. By shifting the absorption and scattering, the color of nanoparticle dispersions and films can also be tuned: for example, solutions of spherical gold nanoparticles are ruby red in color due to the strong scattering and absorption in the green region of the spectrum, while solutions of silver nanoparticles are yellow due to the plasmon resonance in the blue region of the spectrum (red and green light is unaffected). See our Color Engineering article for more examples of how scattering and absorption affect the perceived color of nanomaterials.
The reason for the unique spectral response of silver and gold nanoparticles is that specific wavelengths of light can drive the conduction electrons in the metal to collectively oscillate, a phenomenon known as a surface plasmon resonance (SPR). When these resonances are excited, absorption and scattering intensities can be up to 40x higher than identically sized particles that are not plasmonic. The brightness and tunability of plasmonic nanoparticle optical properties make them highly useful in numerous applications such as molecular detection, solar energy materials, and cancer detection and treatment.
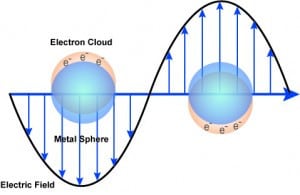
| Schematic of surface plasmonc resonance where the free conduction electrons in the metal nanoparticle are driven into oscillation due to strong coupling with incident light. |
Plasmon Resonance Tutorial
Noble metal nanoparticles support surface plasmons (oscillations of the conduction electrons at the nanoparticle surface) that result in extraordinary optical properties that are not exhibited by any other class of material. The basis for the effect is the plasmon resonance of the free electrons in the metal nanoparticle, which can be understood by studying the polarizability (the ease with which charges, such as the conduction electrons on the metal nanoparticle surface, undergo charge distribution and form partial dipoles). For a spherical nanoparticle, the quasi-static polarizability of the nanoparticle is given by:
![]()
Where ε1 is the wavelength dependent dielectric function of the nanoparticle and ε2 is the dielectric function of the medium which remains roughly constant regardless of wavelength. When the condition Re{ε1} = -2ε2 is satisfied, the particle is driven into resonance resulting in a strong increase in the absorption and/or scattering at that wavelength.
The resonance condition depends on the wavelength dependent dielectric function of the nanoparticle as well as the dielectric function of the medium. Consequently, the nanoparticle optical properties are highly dependent on material composition, size, and the medium in which the particles are embedded. Both the shape and peak resonance wavelength of the nanoparticle plasmon resonance is influenced by the local refractive index. When particles are in water (n = 1.33) the peak resonance of 80 nm Ag particles predicted by Mie Theory is ~445 nm. In air (n = 1.00) the peak wavelength of the plasmon resonance is predicted to be ~380 nm, a blue-shift of 65 nm. However, if the silver particle is coated with a shell of a material that has the same refractive index as water, the peak plasmon wavelength will be restored to ~445 nm. By adjusting the thickness of the shell, the peak resonance of coated nanoparticles can be tuned to any wavelength between these two extremes. To observe this effect for other particle sizes, compositions and refractive indices, see our online Mie Theory calculator which allows you to calculate and view the theoretical optical response of many metal and metal oxide nanoparticles.
Nanoparticle optical properties are also sensitive to the proximity of other plasmonic materials. When two or more plasmonic nanoparticles are near each other (with edge-to-edge separations of one particle diameter or less) their surface plasmons couple as the conduction electrons on each particle surface collectively oscillate. This effect is similar to molecular orbital theory in that plasmon coupling results in the oscillating electrons assuming the lowest energy state, causing the plasmon resonance wavelength of the coupled particles to red-shift to longer wavelengths (lower energies). This coupling effect is responsible for the dramatic changes in the visible color of plasmonic nanoparticle solution when nanoparticles aggregate and also the basis of many different types of plasmonic nanoparticle sensors.
Modeling Plasmonic Nanoparticle Optical Properties
Modeling can be used to predict the optical properties of a nanoparticle of a given size and shape. For example, we have developed a method for the synthesis of gold nanorods that have optical properties correlated to the rod length and the rod aspect ratio (length:width). Because the length and width can be controlled during the fabrication process, modeling can be used to select target geometries that will resonate at a desired wavelengths (e.g. with a specific laser line).
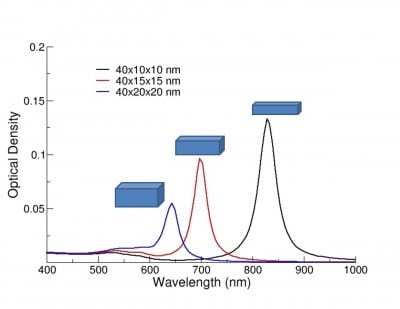
Numerically modeled extinction spectra of gold nanorods of varying aspect ratio.
At nanoComposix, we also use modeling for quality control (QC). After fabricating nanoparticles, particle size is characterized using electron microscopy, and measured optical density (measured by UV-Visible spectroscopy) is compared to the optical density as determined from Mie theory or DDA simulations, described below. Measured (dashed lines) and theoretical (solid lines) optical efficiency of 80 nm NanoXact silver (blue) and gold (red) are displayed in the figure below. The measured optical efficiencies are within 2% of the theoretical maxima, demonstrating that the particles are highly monodisperse and have uniform spherical shapes.
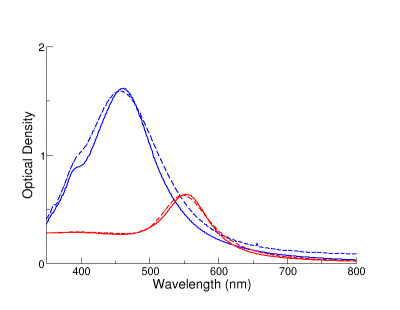
Comparison of measured (dashed) and numerically modeled (solid) extinction spectra 80 nm gold and silver BioPure nanoparticles.
MIE THEORY
Mie theory is not actually a theory, but rather is the analytical solution of Maxwell’s equations for the scattering of light by a spherical particle. Mie theory can be used to calculate the scattering from spheres of any diameter at any wavelength of light. While classical Mie theory assumed that the sphere would be composed of a single material, more recently, Mie theory has been adapted to solve light scattering from layered spheres. At nanoComposix, we have written a custom Mie theory code to calculate the extinction, absorption, and scattering from metal and dielectric nano- and micro-particles. Our online Mie Theory calculator allows you to choose nanoparticle size, composition, and the properties of the media surrounding the particles, and calculate the scattering and absorption spectrum.
DISCRETE DIPOLE APPROXIMATION
Mie theory can only be used to calculate the scattering of light from spherical particles and other methods are needed to compute the scattering of light by nonspherical shapes. Analytical solutions to Maxwell’s equations cannot be calculated for all geometries and alternative methods such as the Discrete Dipole Approximation are used to calculate the extinction, scattering, and absorption of other particle shapes. In DDA, a particle is subdivided into an array of polarizable cubes in a method similar to the one used to generate a 2-D grid or mesh for computational fluid dynamics. The response to light is calculated by calculating the response of a single dipole in the center of each cube to both the incident light, and to the light scattered from each of the other cubes. This iterative process can require a significant amount of computing time that depends upon both the size and shape of the nanoparticle and the dimensions of the cubic grid.
For help selecting a plasmonic nanoparticle that has the correct optical response for your application, please see our product selection page or contact us.